Ruby AVL
An AVL tree, named after the creaters: Adelson-Velsky and Landis, is a self-balancing binary search tree. In an AVL tree, if the depth of the either of a nodes subtrees differ by more than one, rebalancing is done to correct it. A Binary Search Tree (BST) is a special type of binary tree in which the left child of a node has a value less than the node’s value and the right child has a value greater than the node’s value. This property is called the BST property and it makes it possible to efficiently lookup a certain node in the tree, because at every node you half the remaining number of possible candidates. However, when a node is added, it is possible that one subtree becomes bigger than the other, which is where the balancing comes into play.
This is a Ruby gem, so it is entirely written in Ruby. As of last check, it has ~4500 downloads on RubyGems.org.
Code
module AVLTree
class Node
attr_accessor :data, :left, :right
def initialize(data)
@data = data
@left = nil
@right = nil
end
end
end
The Node is the essential component of the tree. This implementation allows any Ruby object to be placed into a Node. However, comparison of the objects needs to be done on an attribute, otherwise the tree won't be able to judge which sub-tree to insert the Node to. This is done easily by implementing the method #compare_to on the object:
class Person
attr_accessor :name
def compare_to(other_person)
this.name <=> other_person.name
end
end
module AVLTree
class BSTree
attr_reader :root
def initialize(root = nil)
@root = root
end
# Starts the search for the insertion at the root of
# the tree. Set the new root at the end if it has changed.
def insert_item(item)
@root = add_to_tree(item, @root)
end
# Starts the search for the deletion at the root of
# the tree. Set the new root at the end if it has changed.
def remove_item(item)
@root = remove_from_tree(item, @root)
end
# Starts the count at the root node.
def number_of_nodes
node_count(@root)
end
# Starts the count of the depth at the root node.
def depth_of_tree
tree_depth(@root, 0)
end
private
# If the current node is null then a new Node object is created and item
# is passed in as a constructor. If item is smaller than the data stored
# in the current node then :add_to_tree is called recursively to traverse
# the left-sub tree until the node is null. The same thing happens if the
# item is larger, but the right sub-tree is traversed. If item is neither
# larger nor smaller then it must be equal, in which case an error will be
# raised to inform the user of duplication.
def add_to_tree(item, node)
if node.nil?
return Node.new(item)
elsif compare(item, node.data) < 0
node.left = add_to_tree(item, node.left)
elsif compare(item, node.data) > 0
node.right = add_to_tree(item, node.right)
else
puts 'Duplicate entry. Skipping: %s' % item
end
return node
end
# If the current node is null then the tree is empty or the item isn't in it.
# If item is smaller or larger than current node like above, if it's neither then
# it must be equal so checks are made to see how many children that node has. If
# it has two then a the value of the node is swapped with the value of the
# smallest item in it's right-sub tree, then removeItem is called again but this time
# on the value in the right sub-tree. If the node has less than two children
# another check is made: if the left child is not null, the value of the node is
# equal to that value, otherwise it's equal to the value of the right child.
def remove_from_tree(item, node)
return if node.nil?
if compare(item, node.data) < 0
node.left = remove_from_tree(item, node.left)
elsif compare(item, node.data) > 0
node.right = remove_from_tree(item, node.right)
elsif node.left && node.right
node.data = least_item(node.right).data
node.right = remove_from_tree(node.data, node.right)
else
node = node.left ? node.left : node.right
end
return node
end
# Comparison of two objects. Will return -1 if item_one is less than item_two, 0 if
# they are equal, and 1 if item_one is greater than item_two. First checks if object
# has it's own comparison logic, if not, uses core Ruby comparision.
def compare(item_one, item_two)
begin
item_one.compare_to(item_two)
rescue NoMethodError
item_one <=> item_two
end
end
# Recursively finds the lowest item in a nodes left subtree.
def least_item(node)
return unless node
return node unless node.left
least_item(node.left)
end
# Traverses the tree and returns the sum of the nodes.
def node_count(node)
node.nil? ? 0 : 1 + node_count(node.left) + node_count(node.right)
end
# Traverses the tree and calculates the depth of the longest sub-tree
def tree_depth(node, depth)
node.nil? ? 0 : depth + max(height(node.left), height(node.right))
end
# Calculates the height of the node using it's leaves. Initial check to see if
# node is nil which means it has a height of 0.
def height(node)
node.nil? ? 0 : 1 + max(height(node.left), height(node.right))
end
# Converts parameters to an Array then calls Enumerable#max on them to return
# the largest element.
def max(*values)
values.max
end
end
end
AVLTree::BSTree is the standard binary search tree, which allows insertion/removal operations, but will not balance. These are best used when the data is complete prior to building and nothing needs to be added afterwards. Searching these trees is fast and efficient while they remain unchanged.
require_relative 'bs_tree'
module AVLTree
class AVLTree < BSTree
# Public interfaces implemented in superclass
private
# Calls superclass (BSTree) method passing in parameters
# recieved from caller. Passes in the returned value of
# BSTree#add_to_tree to :rebalance and returns final result.
def add_to_tree(item, node)
return rebalance(super(item, node))
end
# Calls superclass (BSTree) method passing in parameters
# recieved from caller. Passes in the returned value of
# BSTree#remove_from_tree to :rebalance and returns final
# result.
def remove_from_tree(item, node)
return rebalance(super(item, node))
end
# Checks the balance factor of the node and rotates the tree
# if inbalanced in any way. Balance algorithm:
# IF tree is right heavy
# IF tree's right subtree is left heavy (Right Left Case)
# Perform Double Left rotation
# ELSE (Right Right Case)
# Perform Single Left rotation
# ELSE IF tree is left heavy
# IF tree's left subtree is right heavy (Left Right Case)
# Perform Double Right rotation
# ELSE (Left Left Case)
# Perform Single Right rotation
# END IF
def rebalance(node)
if balance_factor(node) >= 2
if (balance_factor(node.left) < 0)
return double_rotate_right(node)
else
return rotate_right(node)
end
elsif balance_factor(node) <= -2
if (balance_factor(node.right) > 0)
return double_rotate_left(node)
else
return rotate_left(node)
end
else
return node
end
end
# Node becomes the left subtree of it's right subtree.
def rotate_left(node)
new_node = node.right
node.right = new_node.left
new_node.left = node
return new_node
end
# Right rotation performed on node's right subtree before
# node is rotated left.
def double_rotate_left(node)
node.right = rotate_right(node.right)
return rotate_left(node)
end
# Node becomes the right subtree of it's left subtree.
def rotate_right(node)
new_node = node.left
node.left = new_node.right
new_node.right = node
return new_node
end
# Left rotation performed on node's left subtree before
# node is rotated right.
def double_rotate_right(node)
node.left = rotate_left(node.left)
return rotate_right(node)
end
# Calculates the height of the left subtree, then subtracts the height of the
# right subtree to produce the balance factor for the node.
def balance_factor(node)
node.nil? ? 0 : (height(node.left) - height(node.right))
end
end
end
AVLTree::AVLTree is the purpose of this library. It provides the same value as the AVLTree::BSTree, but allows insert and remove operations to maintain the efficiency of the tree. However, this efficiency comes with processing overhead as the balance will be done for every node whenever the tree is modified. It is preferable to if new nodes are added, or some removed, after the tree is built.
module AVLTree
class BSTreeTraversal
def pre_order_array(root_node, attribute = nil)
pre_order(root_node, attribute, [])
end
def pre_order_string(root_node, attribute = nil)
pre_order(root_node, attribute, []).join(', ')
end
def in_order_array(root_node, attribute = nil)
in_order(root_node, attribute, [])
end
def in_order_string(root_node, attribute = nil)
in_order(root_node, attribute, []).join(', ')
end
def post_order_array(root_node, attribute = nil)
post_order(root_node, attribute, [])
end
def post_order_string(root_node, attribute = nil)
post_order(root_node, attribute, []).join(', ')
end
private
def pre_order(node, attribute, node_list)
unless node.nil?
node_list << (attribute ? node.data.send(attribute) : node.data)
pre_order(node.left, attribute, node_list)
pre_order(node.right, attribute, node_list)
end
return node_list
end
def in_order(node, attribute, node_list)
unless node.nil?
in_order(node.left, attribute, node_list)
node_list << (attribute ? node.data.send(attribute) : node.data)
in_order(node.right, attribute, node_list)
end
return node_list
end
def post_order(node, attribute, node_list)
unless node.nil?
post_order(node.left, attribute, node_list)
post_order(node.right, attribute, node_list)
node_list << (attribute ? node.data.send(attribute) : node.data)
end
return node_list
end
end
end
Finally, the traversals are three methods of printing the data from the nodes in the tree. Each of the iterates over the tree, but does do in different order:
- Pre-order traversal: visit the nodes in the order root-left-right, meaning for any subtree in the path, root is processed as the node is visited, left node is visited second, followed by right node.
- In-order traversal: visit the nodes in the order left-root-right, meaning for any subtree in the path, left node must be visited first followed by root, then finally the right node. Prints the values in ascending order.
- Post-order traversal: visit the nodes in the order left-right-root, meaning for any subtree in the path, left node must be visited first, followed by the right node, and root is not processed until the children are.
Example
We will use the example from the tests contained in the gem and add some visualisations. Consider the following code that produces a AVL tree:
tree = AVLTree::AVLTree.new()
tree.insert_item(25)
tree.insert_item(50)
tree.insert_item(100)
tree.insert_item(80)
tree.insert_item(70)
tree.insert_item(57)
tree.insert_item(72)
tree.insert_item(77)
tree.insert_item(94)
tree.insert_item(63)
tree.insert_item(30)
tree.insert_item(30)
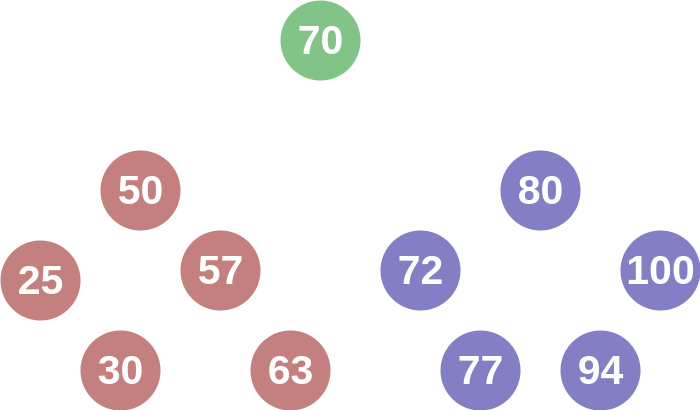
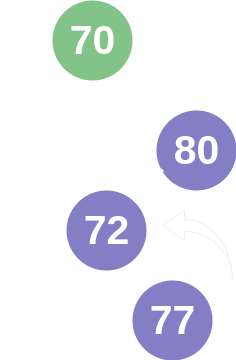
As you can see, a balanced tree is produced with the left subtree of any node containing values that are less than the node's value, and a right subtree with greater values.
If one was to remove the nodes with values 25 and 30, then the node with the value of 50 would become unbalanced; with 0 nodes in the left and 2 nodes in the right subtrees. The AVL tree would perform a "left rotation" on the node with value 50, so that the node would have 1 node in each subtree.
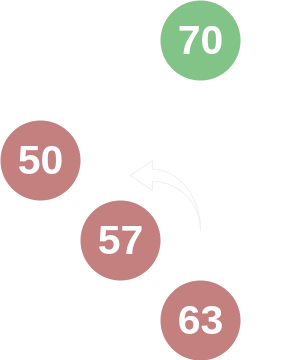
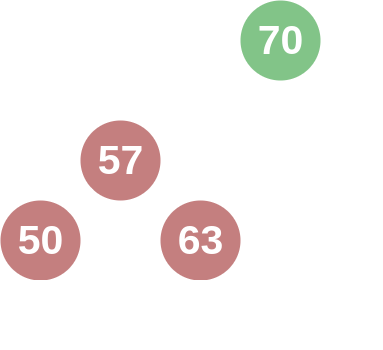
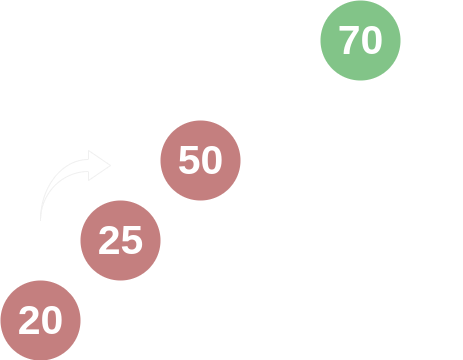
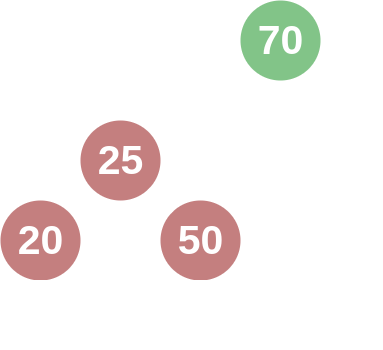
Similarly, if one was to add a node with the value 20 and remove the nodes with values 30, 57, and 63, then the subtree of the node with the value 50 would be imbalanced on the left side. The AVL tree would then perform a "right rotation" on the node with value 50 so that it again would have 1 node in each subtree.
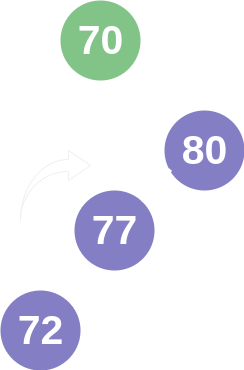
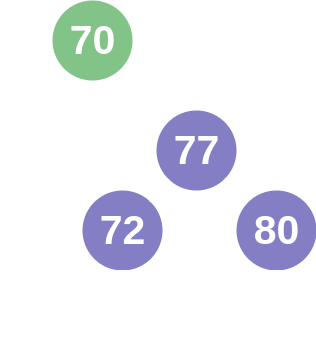
A more complex solution occurs when a node cannot be balanced by a single rotation. If one was to remove the nodes with values 72 and 77, then the node with value 80 would become imbalanced on the right side. However, due to the composition of the tree, a single "left rotation" would cause the node with value 100 to have a node with a smaller value in it's right subtree. This breaks the fundamental design of a binary search tree, so the AVL tree would perform a "double left rotation" to finish in a balanced state. This name is confusing, because it doesn't mean two left rotations. What happens is that a "right rotation" performed on node's right subtree before the node is rotated left. In this example, that would swap the places of nodes with values 94 and 100.
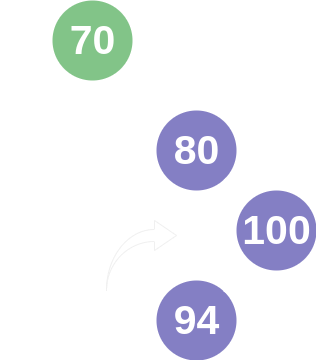
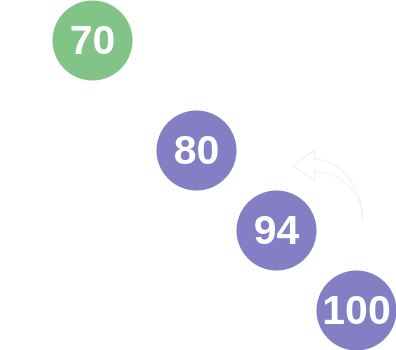
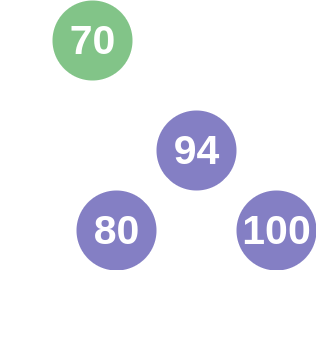
The final balancing operation is similar to the last, but for a heavy left subtree. If one was to remove nodes with values 94 and 100, then the node 80 would again be unbalanced. However, a single right rotation would result in the node with value 72 having a node with a greater value in it's left subtree. In this case, like above, a double rotation would occur, but a "double right rotation". This is when a "left rotation" is performed on node's left subtree before node is rotated right.